Advertisements
Advertisements
प्रश्न
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other an angle of 60º.
उत्तर १
In order to draw the pair of tangents, we follow the following steps.
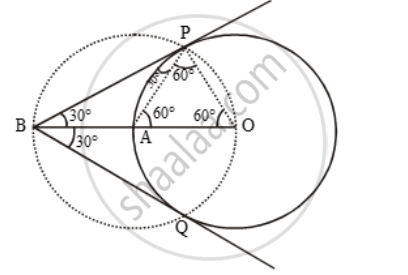
Step I: Take a point O on the plane of the paper and draw a circle of radius OA = 5 cm.
Step II: Produce OA to B such that OA = AB = 5 cm.
Step III: Taking A as the centre draw a circle of radius AO = AB = 5 cm.
Suppose it cuts the circle drawn in step I at P and Q.
Step IV: Join BP and BQ to get the desired tangents.
Justification: In OAP, we have
OA = OP = 5 cm (= Radius) Also,
AP = 5 cm (= Radius of circle with centre A)
∴ ∆OAP is equilateral.
⇒ ∠PAO = 60º ⇒ ∠BAP = 120º
In ∆BAP, we have
BA = AP and ∠BAP = 120º
∴ ∠ABP = ∠APB = 30º ⇒ ∠PBQ = 60º
उत्तर २
The tangents can be constructed in the following manner:
Step 1
Draw a circle of radius 5 cm and with centre as O.
Step 2
Take a point A on the circumference of the circle and join OA. Draw a perpendicular to OA at point A.
Step 3
Draw a radius OB, making an angle of 120° (180° − 60°) with OA.
Step 4
Draw a perpendicular to OB at point B. Let both the perpendiculars intersect at point P. PA and PB are the required tangents at an angle of 60°.
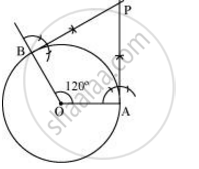
Justification
The construction can be justified by proving that ∠APB = 60°
By our construction
∠OAP = 90°
∠OBP = 90°
And ∠AOB = 120°
We know that the sum of all interior angles of a quadrilateral = 360°
∠OAP + ∠AOB + ∠OBP + ∠APB = 360°
90° + 120° + 90° + ∠APB = 360°
∠APB = 60°
This justifies the construction.
संबंधित प्रश्न
In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°,
find the value of x, y and z.

Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents form the point P to the circle
Use rule and compass only for answering this question.
Draw a circle of radius 4 cm. Mark the centre as O. Mark a point P outside the circle at a distance of 7 cm from the centre. Construct two tangents to the circle from the external point P.
Measure and write down the length of any one tangent.
Draw a circle with centre O and radius 3 cm. Take a point P outside the circle. Draw tangents to the circle from P without using the centre and using only ruler and compasses.
Draw a circle at a radius of 3 cm. Take a point at 5.5 cm from the center at the circle. From point P, draw two tangents to the circle.
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
