Advertisements
Advertisements
प्रश्न
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q. Give the justification of the construction.
उत्तर १
The tangent can be constructed on the given circle as follows.
Step 1
Taking any point O on the given plane as centre, draw a circle of 3 cm radius.
Step 2
Take one of its diameters, PQ, and extend it on both sides. Locate two points on this diameter such that OR = OS = 7 cm
Step 3
Bisect OR and OS. Let T and U be the mid-points of OR and OS respectively.
Step 4
Taking T and U as its centre and with TO and UO as radius, draw two circles. These two circles will intersect the circle at point V, W, X, Y respectively. Join RV, RW, SX, and SY. These are the required tangents.

Justification
The construction can be justified by proving that RV, RW, SY, and SX are the tangents to the circle (whose centre is O and radius is 3 cm). For this, join OV, OW, OX, and OY.
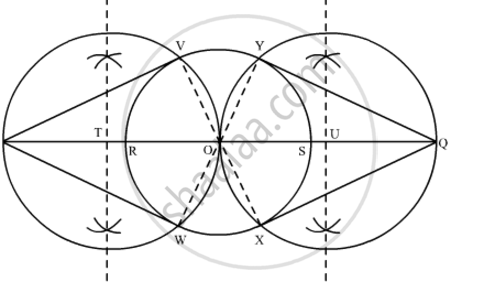
∠RVO is an angle in the semi-circle. We know that angle in a semi-circle is a right angle.
∴ ∠RVO = 90°
⇒ OV ⊥ RV
Since OV is the radius of the circle, RV has to be a tangent to the circle.
Similarly, it can be shown that RW, SX, and SY are the tangents of the circle.
उत्तर २
Given that
Construct a circle of radius 3 cm, and let a point P and Q extended diameter each at distance of 7cm from its centre. Construct the pair of tangents to the circle from these two points P and Q.
We follow the following steps to construct the given
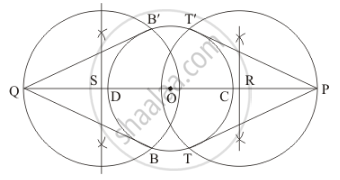
Step of construction
Step: I- First of all we draw a circle of radius = 3 cm.
Step: II- Make a line CD = diameter = 6 cm.
Step: III-Extend the line CD in such a way that point CP = DQ = 7 cm
Step: IV- CP at a distance of OP = 7 + 3 = 10 cm, and join OP draw a right bisector of OP, intersecting OP at R.
Step V:- Similarly, DQ at a distance of OQ = 7 + 3 = 10 cm, and join OQ draw a right bisector of OQ, intersecting OQ at S.
Step VI: Taking R and S as centre and radius OS = OR, draw a circle to intersect the given circle at T and T’
B and B ’respectively.
Step: VII- Joins PT and PT’ as well as QB and QB’ to obtain the require tangents.
Thus, PT and P'T' , QB and QB' are the required tangents.
संबंधित प्रश्न
Draw a circle of radius 3 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60º.
In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
1) AB.
2) the length of tangent PT.

Draw a circle circumscribing a regular hexagon with side 5 cm.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw a circle with centre O and radius 2.5 cm. Take a point P at a distance of 6 cm from the centre. Using ruler and compasses only construct the tangents to the circle from the point P.
Use a ruler and a pair of compasses to construct ΔABC in which BC = 4.2 cm, ∠ ABC = 60°, and AB 5 cm. Construct a circle of radius 2 cm to touch both the arms of ∠ ABC of Δ ABC.
Draw a circle of radius 4 cm. Take a point P outside the circle without using the center at the circle. Draw two tangents to the circle from point P.
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
A pair of tangents can be constructed to a circle inclined at an angle of 170°.
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
