Question

Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.

Answer 1

In order to do the desired construction,

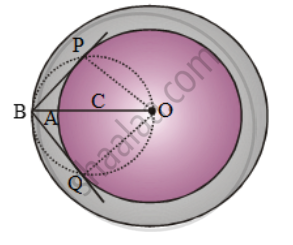
we follow the following steps:

Step I: Take a point O on the plane of the paper and draw a circle of radius OA = 4 cm. Also, draw a concentric circle of radius OB = 6 cm.

Step II: Find the mid-point C of OB and draw a circle of radius OC = BC. Suppose this circle intersects the circle of radius 4 cm at P and Q.

Step III: Join BP and BQ to get the desired tangents from a point B on the circle of radius 6 cm.

By actual measurement, we find the

BP = BQ = 4.5 cm

Justification: In ∆BPO, we have

OB = 6 cm and OP = 4 cm

`OB^2 = BP^2 + OP^2 ` [Using Pythagoras theorem]

`\Rightarrow BP=\sqrt{OB^{2}-OP^{2}`

`\Rightarrow \sqrt{36-16}=\sqrt{20}=4.47 ~= 4.5 `

Similarly, BQ = 4.47cm ≈ 4.5 cm

Answer 2

Tangents on the given circle can be drawn as follows.

Step 1

Draw a circle of 4 cm radius with centre as O on the given plane.

Step 2

Draw a circle of 6 cm radius taking O as its centre. Locate a point P on this circle and join OP.

Step 3

Bisect OP. Let M be the mid-point of PO.

Step 4

Taking M as its centre and MO as its radius, draw a circle. Let it intersect the given circle at the points Q and R.

Step 5

Join PQ and PR. PQ and PR are the required tangents.

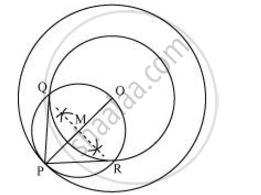
It can be observed that PQ and PR are of length 4.47 cm each.

In ΔPQO,

Since PQ is a tangent,

∠PQO = 90°

PO = 6 cm

QO = 4 cm

Applying Pythagoras theorem in ΔPQO, we obtain

PQ² + QO² = PQ²

PQ² + (4)² = (6)²

PQ² + 16 = 36

PQ² = 36 − 16

PQ² = 20

PQ = `2sqrt5`

PQ = 4.47 cm

Justification

The construction can be justified by proving that PQ and PR are the tangents to the circle (whose centre is O and radius is 4 cm). For this, let us join OQ and OR.

∠PQO is an angle in the semi-circle. We know that angle in a semi-circle is a right angle.

∴ ∠PQO = 90°

⇒ OQ ⊥ PQ

Since OQ is the radius of the circle, PQ has to be a tangent of the circle. Similarly, PR is a tangent of the circle.