Advertisements
Advertisements
प्रश्न
Draw a circle circumscribing a regular hexagon with side 5 cm.
उत्तर
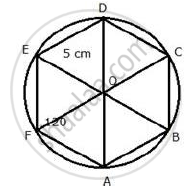
Steps of construction:
- Draw a regular hexagon ABCDEF with each side equal to 5 cm and each interior angle 120°.
- Join its diagonals AD, BE and CF intersecting each other at O.
- With centre as O and radius OA, draw a circle which will pass through the vertices A, B, C, D, E and F.
This is the required circumcircle.
APPEARS IN
संबंधित प्रश्न
Draw a right triangle ABC in which AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD perpendicular from B on AC and draw a circle passing through the points B, C and D. Construct tangents from A to this circle.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Draw two tangents to a circle of radius 3.5 cm form a point P at a distance of 6.2 cm form its centre.
Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm , which are inclined to each other at an angle of 60° .
A park is of the shape of a circle of diameter 7 m. It is surrounded by a path of width of 0·7 m. Find the expenditure of cementing the path, if its cost is Rs 110 per sq. m ?
Draw a circle at a radius of 3 cm. Take a point at 5.5 cm from the center at the circle. From point P, draw two tangents to the circle.
Use a ruler and a pair of compasses to construct ΔABC in which BC = 4.2 cm, ∠ ABC = 60°, and AB 5 cm. Construct a circle of radius 2 cm to touch both the arms of ∠ ABC of Δ ABC.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of 3 cm from the centre.
