Advertisements
Advertisements
प्रश्न
Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm , which are inclined to each other at an angle of 60° .
उत्तर
Steps of Construction
Step 1: Draw a circle with center O and radius 3c m.
Step 2: Draw any diameter AOB of the circle.
Step 3: Construct ∠BOC = 60° such that radius OC cuts the circle at C.
Step 4: Draw AM ⊥ AB and CN ⊥ OC. Suppose AM and CN intersect each other at P.
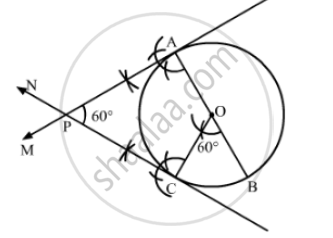
Here, AP and CP are the pair of tangents to the circle inclined to each other at an angle of 60°.
APPEARS IN
संबंधित प्रश्न
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Draw a circle of radius 3 cm. Form a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents
Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.
A park is of the shape of a circle of diameter 7 m. It is surrounded by a path of width of 0·7 m. Find the expenditure of cementing the path, if its cost is Rs 110 per sq. m ?
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Draw a circle with centre O and radius 2.5 cm. Take a point P at a distance of 6 cm from the centre. Using ruler and compasses only construct the tangents to the circle from the point P.
Using ruler and compasses only, draw tangents to a circle of radius 3 cm from a point 5 cm from the centre. What is the length of each of them ?
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
