Advertisements
Advertisements
प्रश्न
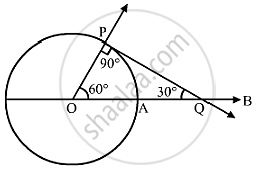
Draw a circle of radius 32 cm. Draw a tangent to the circle making an angle 30° with a line passing through the centre.
उत्तर
Steps Of construction:
Step 1: Draw a circle with center O and radius 3 cm.
Step 2: Draw radius OA and produce it to B.
Step 3: Make ∠AOP = 60°
Step 4: Draw PQ ⊥ OP,meeting OB at Q.
Step 5: Then, PQ is the desired tangent, such that ∠OQP = 30°
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Draw a circle with center O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.
Draw a circle of radius 4.2. Draw a pair of tangents to this circle inclined to each other at an angle of 45°
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Draw a circle of radius 4 cm and take a point Pon its circumference. Construct a tangent to the circle at P.
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
Construct a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60°.
