Advertisements
Advertisements
प्रश्न
Construct a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60°.
उत्तर
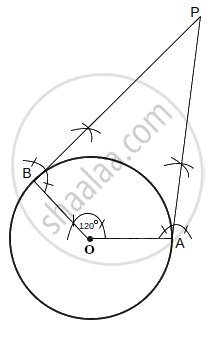
Steps of construction:
- Draw a circle with a radius of 3 cm with the centre as O.
- Take point A on the circumference of the circle and join OA. Draw a perpendicular at OA at point A.
- Draw a radius OB, making an angle of 120° [180° – 60°] with OA.
- Draw a perpendicular to OB at point B. Let both the perpendicular intersect at point P. PA and PB are the required tangents at an angle of 60°.
APPEARS IN
संबंधित प्रश्न
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circles. Give the justification of the construction.
Draw an inscribing circle of a regular hexagon of side 5.8 cm.
Draw a circle of radius 3 cm. Form a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents
Use rule and compass only for answering this question.
Draw a circle of radius 4 cm. Mark the centre as O. Mark a point P outside the circle at a distance of 7 cm from the centre. Construct two tangents to the circle from the external point P.
Measure and write down the length of any one tangent.
Draw two circles with radii 2.5 cm and 4 cm and with their centres 7 cm apart.
Draw a direct common tangent and a transverse common tangent. Calculate the length of the direct common tangent.
Draw a circle of radius 4 cm. From a point 6 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
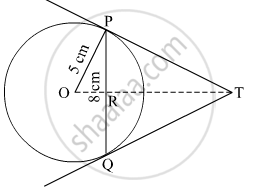
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60º. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
