Advertisements
Advertisements
प्रश्न
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Give the justification of the construction.
उत्तर १
A pair of tangents to the given circle can be constructed as follows.
Step 1
Taking any point O of the given plane as centre, draw a circle of 6 cm radius. Locate a point P, 10 cm away from O. Join OP.
Step 2
Bisect OP. Let M be the mid-point of PO.
Step 3
Taking M as centre and MO as radius, draw a circle.
Step 4
Let this circle intersect the previous circle at point Q and R.
Step 5
Join PQ and PR. PQ and PR are the required tangents.
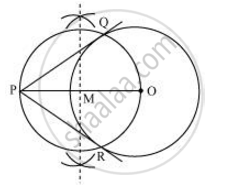
The lengths of tangents PQ and PR are 8 cm each.
Justification
The construction can be justified by proving that PQ and PR are the tangents to the circle (whose centre is O and radius is 6 cm). For this, join OQ and OR.
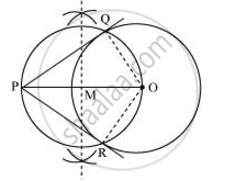
∠PQO is an angle in the semi-circle. We know that angle in a semi-circle is a right angle.
∴ ∠PQO = 90°
⇒ OQ ⊥ PQ
Since OQ is the radius of the circle, PQ has to be a tangent of the circle. Similarly, PR is a tangent of the circle.
उत्तर २
Given that
Construct a circle of radius 6 cm, and let a point P = 10 cm form its centre, construct the pair of tangents to the circle.
Find the length of tangents.
We follow the following steps to construct the given
Step of construction
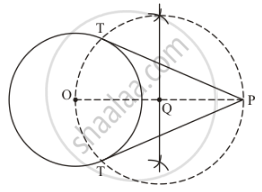
Step: I- First of all we draw a circle of radius AB = 6 cm.
Step: II- Make a point P at a distance of OP = 10 cm, and join OP.
Step: III -Draw a right bisector of OP, intersecting OP at Q .
Step: IV- Taking Q as centre and radius OQ = PQ, draw a circle to intersect the given circle at T and T’.
Step: V- Joins PT and PT’ to obtain the require tangents.
Thus, PT and P'T' are the required tangents.
Find the length of tangents.
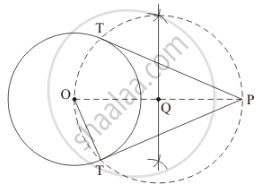
As we know that OT ⊥ PT and ΔOPT is right triangle.
Therefore,
OT = 6cm and PO = 10cm
In ΔOPT,
PT2 = OP2 - OT2
PT2 = 102 - 62
PT2 = 100 - 36
PT2 = 64
`PT = sqrt64=8`
Thus, the length of tangents = 8 cm.
APPEARS IN
संबंधित प्रश्न
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
- A circle of radius 2.5 cm, passing through A and C.
- Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
1) AB.
2) the length of tangent PT.

Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Draw a circle of radius 4 cm and take a point Pon its circumference. Construct a tangent to the circle at P.
Draw a circle at a radius of 4 cm. Take a point on it. Without using the centre at the circle, draw a tangent to the circle at point P.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is ______.
You are given a circle with radius ‘r’ and center O. You are asked to draw a pair of tangents which are inclined at an angle of 60° with each other. Refer to the figure and select the option which would lead us to the required construction. d is the distance OE.

Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Draw a circle of radius 2.5 cm. Construct a pair of tangents from a point Pat a distance of 6 cm from the centre of the circle.
