Question

Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other an angle of 60º.

Answer 1

In order to draw the pair of tangents, we follow the following steps.

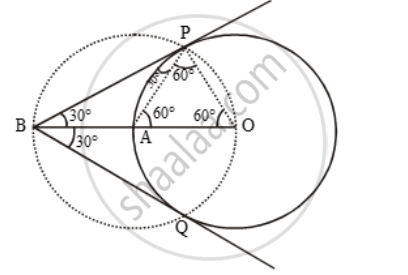
Step I: Take a point O on the plane of the paper and draw a circle of radius OA = 5 cm.

Step II: Produce OA to B such that OA = AB = 5 cm.

Step III: Taking A as the centre draw a circle of radius AO = AB = 5 cm.

Suppose it cuts the circle drawn in step I at P and Q.

Step IV: Join BP and BQ to get the desired tangents.

Justification: In OAP, we have

OA = OP = 5 cm (= Radius) Also,

AP = 5 cm (= Radius of circle with centre A)

∴ ∆OAP is equilateral.

⇒ ∠PAO = 60º ⇒ ∠BAP = 120º

In ∆BAP, we have

BA = AP and ∠BAP = 120º

∴ ∠ABP = ∠APB = 30º ⇒ ∠PBQ = 60º

Answer 2

The tangents can be constructed in the following manner:

Step 1

Draw a circle of radius 5 cm and with centre as O.

Step 2

Take a point A on the circumference of the circle and join OA. Draw a perpendicular to OA at point A.

Step 3

Draw a radius OB, making an angle of 120° (180° − 60°) with OA.

Step 4

Draw a perpendicular to OB at point B. Let both the perpendiculars intersect at point P. PA and PB are the required tangents at an angle of 60°.

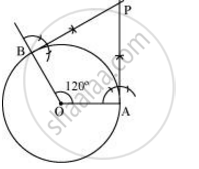
Justification

The construction can be justified by proving that ∠APB = 60°

By our construction

∠OAP = 90°

∠OBP = 90°

And ∠AOB = 120°

We know that the sum of all interior angles of a quadrilateral = 360°

∠OAP + ∠AOB + ∠OBP + ∠APB = 360°

90° + 120° + 90° + ∠APB = 360°

∠APB = 60°

This justifies the construction.