Advertisements
Advertisements
प्रश्न
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
उत्तर
The tangents can be constructed on the given circles as follows.
Step 1
Draw a line segment AB of 8 cm. Taking A and B as centre, draw two circles of 4 cm and 3 cm radius.
Step 2
Bisect the line AB. Let the mid-point of AB be C. Taking C as centre, draw a circle of AC radius which will intersect the circles at points P, Q, R, and S. Join BP, BQ, AS, and AR. These are the required tangents.

Justification
The construction can be justified by proving that AS and AR are the tangents of the circle (whose centre is B and radius is 3 cm) and BP and BQ are the tangents of the circle (whose centre is A and radius is 4 cm). For this, join AP, AQ, BS, and BR.
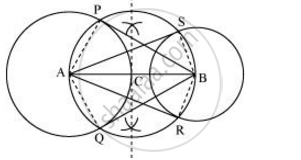
∠ASB is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.
∴ ∠ASB = 90°
⇒ BS ⊥ AS
Since BS is the radius of the circle, AS has to be a tangent of the circle. Similarly, AR, BP, and BQ are the tangents.
APPEARS IN
संबंधित प्रश्न
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
- A circle of radius 2.5 cm, passing through A and C.
- Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.
Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents form the point P to the circle
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
You are given a circle with radius ‘r’ and center O. You are asked to draw a pair of tangents which are inclined at an angle of 60° with each other. Refer to the figure and select the option which would lead us to the required construction. d is the distance OE.

A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
Construct a tangent to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
Using ruler and compass construct a triangle ABC in which AB = 6 cm, ∠BAC = 120° and AC = 5 cm. Construct a circle passing through A, B and C. Measure and write down the radius of the circle.
