Advertisements
Advertisements
प्रश्न
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

उत्तर
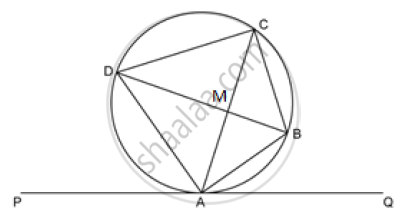
1) `angleBAQ = 30^@`
SinceAB is the bisector of `angleCAQ`
`=> angleCAB = angleBAQ = 30^@`
AD is the bisector of `angle CAP` and P-A-Q,
`angle DAP + angle CAD + angle CAQ = 180^@`
`=> angleCAD + anglle CAD + 60^@ = 180 ^@`
`=> angle CAD = 60^@`
So `angle CAD + angle CAB = 60^@ + 30^@ = 90^@`
Since angle in a semi-circle = 90°
⇒ Angle made by diameter to any point on the circle is 90°
So, BD is the diameter of the circle.
2) SinceBD is the diameter of the circle, so it will pass through the centre.
By Alternate segment theorem
`angle ABD = angle DAC = 60^@`
So, in `angle BMA`,
`angle AMB = 90^@` .........(UseAngleSumProperty)
We know that perpendicular drawn from the centre to a chord of a circle bisects the chord.
`=> angle BMA = angle BMC = 90^@`
In `triangleBMA` and `triangleBMC`
`angleBMA = angleBMC = 90^@`
BM = BM (common side)
AM = CM(perpendicular drawn from the centre to a chord of a circle bisects the chord.)
⇒ ΔBMA ≅ ΔBMC
⇒ AB = BC (SAS congruence criterion)
⇒ ΔABC is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other.
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Draw a circle of radius of 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q ?
Draw a circle of radius 4 cm. From a point 6 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
Draw a circle of radius 4 cm. Take a point P outside the circle without using the center at the circle. Draw two tangents to the circle from point P.
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
A pair of tangents can be constructed to a circle inclined at an angle of 170°.
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
