Advertisements
Advertisements
प्रश्न
Draw a circle of radius 4 cm. Take a point P outside the circle without using the center at the circle. Draw two tangents to the circle from point P.
उत्तर
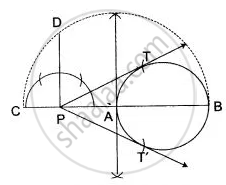
Steps of construction:
(i) Draw a circle of radius 4 cm.
(ii) Take a point P outside the circle and draw a secant PAB, intersecting the circle at A and B.
(iii) Produce AP to C such that AP = CP.
(iv) Draw a semicircle with CB as diameter.
(v) Draw PD and CB intersecting the semi-circle at D.
(vi) With P as centre and PD as a radius draw arcs to intersect the given circle at T and T'.
(vii) Join PT and PT'. Then PT and PT' are the required tangents.
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 3 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60º.
Construct a tangent to a circle of radius 4 cm form a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Draw a circle of radius 4 cm and take a point Pon its circumference. Construct a tangent to the circle at P.
Draw two circles of radii 2.5 cm and 3.5 cm respectively so that their centres are 8 cm apart. Draw direct comm on tangents to the circle.
Draw two circles of radii 3.5 cm and 2 cm respectively so that their centres are 6 cm apart. Draw direct common tangents to the circle and show that they are equal in length.
Draw two circles of radii 3 cm and 3.5 cm, their centres being 8 cm apart. Construct a transverse common tangent and measure its length.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 60°, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be ______.
A pair of tangents can be constructed from a point P to a circle of radius 3.5cm situated at a distance of ______ from the centre.
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
