Advertisements
Advertisements
प्रश्न
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
उत्तर
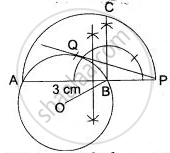
Steps of construction:
1) With centre O and radius = 3 cm, draw a circle.
2) Take any point P outside the circle.
3) Through the external point, P draw a straight line PBA meeting the circle at A and B.
4) Draw a semicircle on AP as diameter.
5) Draw BC ⊥ AP, which intersects the semicircle at C.
6) With centre P and radius, PC draw an arc cutting the circle at Q.
7) Join PQ. Then PQ is the required tangent.
APPEARS IN
संबंधित प्रश्न
Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length.
Draw a circle of radius 3 cm. Take a point at a distance of 5.5 cm from the centre of the circle. From point P, draw two tangents to the circle.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Give the justification of the construction.
Draw a circle with center O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Draw a circle with centre O and radius 2.5 cm. Take a point P at a distance of 6 cm from the centre. Using ruler and compasses only construct the tangents to the circle from the point P.
Draw a circle at a radius of 3 cm. Take a point at 5.5 cm from the center at the circle. From point P, draw two tangents to the circle.
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
Which of the following is not true for a point P on the circle?
A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of 3 cm from the centre.
