Question

Draw a circle at a radius of 3 cm. Take a point at 5.5 cm from the center at the circle. From point P, draw two tangents to the circle.

Answer 1

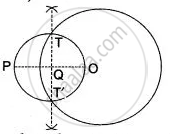
Steps of construction:
(i) Take a point O in the plane paper and draw a circle of radius 3 cm.

(ii) Mark a point P at distance 5.5 cm from the centre O and join OP.

(iii) Draw the right bisector at OP, intersecting OP at Q.

(iv) Taking Q as the centre and OQ = PQ as radius, draw a circle to intersect the given circle at T and T'.

(v) Join PT and PT' to get the required tangent.

Taype (II). Construction of a tangent to a circle from an external point when its centre is known.

Steps of construction:
Let P be the external point from where the tangent are to be drawn to the given circle.
(i) Through P draw a secant PAB to intersect the circle at A and B.

(ii) Join AP to a point C such that AP = DX is equal to the mid-point at AC.

(iii) Draw a semicircle with BC as diameter.

(iv) Draw PD ⊥ BCX intersecting the semicircle at D.

(v) With P as centre and PD as radius draw arcs to intersect the given circle at T and T'.

(vi) Join PT and PT'. Then PT and PT' are the required tangent.