Advertisements
Advertisements
Question
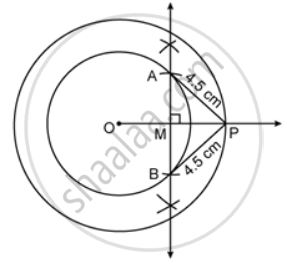
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
Solution
Steps for construction:
- Draw concentric circles of radius 4 cm and 6 cm with centre of O.
- Take point P on the outer circle.
- Join OP.
- Draw perpendicular bisectors of OP where M is the midpoint of OP.
- Take a distance of a point O from the point M and mark arcs from M on the inner circle it cuts at point A and B respectively.
- Join PA and PB.
- We observe that PA and PB are tangents from outer circle to inner circle are equal of a length 4.5 cm each.
APPEARS IN
RELATED QUESTIONS
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Draw a circle of diameter 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Draw two tangents to a circle of radius 3.5 cm form a point P at a distance of 6.2 cm form its centre.
Draw a circle of radius of 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q ?
Draw a circle of radius 4 cm and take a point Pon its circumference. Construct a tangent to the circle at P.
Draw two circles with radii 2.5 cm and 4 cm and with their centres 7 cm apart.
Draw a direct common tangent and a transverse common tangent. Calculate the length of the direct common tangent.
Use a ruler and a pair of compasses to construct ΔABC in which BC = 4.2 cm, ∠ ABC = 60°, and AB 5 cm. Construct a circle of radius 2 cm to touch both the arms of ∠ ABC of Δ ABC.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is ______.
Which of the following is not true for a point P on the circle?
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
