Advertisements
Advertisements
Questions
Draw a right triangle ABC in which AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD perpendicular from B on AC and draw a circle passing through the points B, C and D. Construct tangents from A to this circle.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, and D is drawn. Construct the tangents from A to this circle. Give the justification of the construction.
Solution 1
Follow the given steps to construct the figure.
Step 1
Draw a line BC of 8 cm length.
Step 2
Draw BX perpendicular to BC.
Step 3
Mark an arc at the distance of 6 cm on BX. Mark it as A.
Step 4
Join A and C. Thus, ∆ABC is the required triangle.
Step 5
With B as the centre, draw an arc on AC.
Step 6
Draw the bisector of this arc and join it with B. Thus, BD is perpendicular to AC.
Step 7
Now, draw the perpendicular bisector of BD and CD. Take the point of intersection as O.
Step 8
With O as the centre and OB as the radius, draw a circle passing through points B, C and D.
Step 9
Join A and O and bisect it. Let P be the midpoint of AO.
Step 10
Taking P as the centre and PO as its radius, draw a circle which will intersect the circle at point B and G. Join A and G.
Here, AB and AG are the required tangents to the circle from A.

Solution 2
Consider the following situation. If a circle is drawn through B, D, and C, BC will be its diameter as ∠BDC is of measure 90°. The centre E of this circle will be the mid-point of BC.
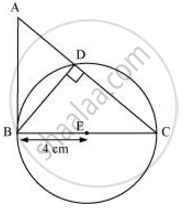
The required tangents can be constructed on the given circle as follows.
Step 1
Join AE and bisect it. Let F be the mid-point of AE.
Step 2
Taking F as centre and FE as its radius, draw a circle which will intersect the circle at point B and G. Join AG.
AB and AG are the required tangents.
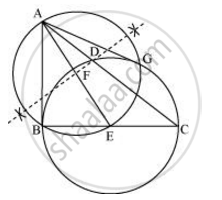
Justification
The construction can be justified by proving that AG and AB are the tangents to the circle. For this, join EG.
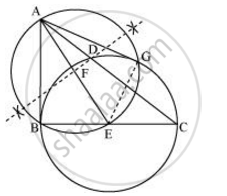
∠AGE is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.
∴ ∠AGE = 90°
⇒ EG ⊥ AG
Since EG is the radius of the circle, AG has to be a tangent of the circle.
Already, ∠B = 90°
⇒ AB ⊥ BE
Since BE is the radius of the circle, AB has to be a tangent of the circle.
APPEARS IN
RELATED QUESTIONS
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other an angle of 60º.
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Draw a circle of radius 4 cm and take a point Pon its circumference. Construct a tangent to the circle at P.
Draw two circles of radii 3 cm and 3.5 cm, their centres being 8 cm apart. Construct a transverse common tangent and measure its length.
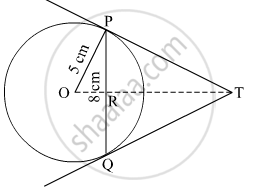
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
