Advertisements
Advertisements
Question
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Solution
Steps of Construction
Step 1. Draw a circle with centre O and radius 4.5 cm.
Step 2. Draw any diameter AOB of the circle.
Step 3. Construct ∠BOC = 45º such that radius OC cuts the circle at C.
Step 4. Draw AM ⊥ AB and CN ⊥ OC. Suppose AM and CN intersect each other at P.
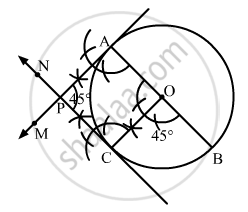
Here, AP and CP are the pair of tangents to the circle inclined to each other at an angle of 45º.
APPEARS IN
RELATED QUESTIONS
Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length.
The bisectors of angles A and B of a scalene triangle ABC meet at O.
- What is the point O called?
- OR and OQ are drawn perpendicular to AB and CA respectively. What is the relation between OR and OQ?
- What is the relation between angle ACO and angle BCO?
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw a circle of radius 3 cm. Form a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
Draw a circle of radius 4 cm. From a point 6 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60º. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
Using ruler and compass construct a triangle ABC in which AB = 6 cm, ∠BAC = 120° and AC = 5 cm. Construct a circle passing through A, B and C. Measure and write down the radius of the circle.
