Advertisements
Advertisements
Question
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.
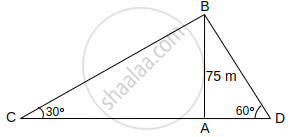
Solution

In ΔBAD,
tan 60° = `("AB")/("AD")`
⇒ `sqrt(3) = 75/("AD")`
⇒ AD = `75/sqrt(3) xx sqrt(3)/sqrt(3)`
= `(75sqrt(3))/3`
= `25sqrt(3)` m ...(i)
and In ΔBAC,
tan 30° = `("AB")/("AC")`
⇒ `1/sqrt(3) = 75/("AC")`
⇒ AC = `75sqrt(3)` m ...(ii)
From equations (i) and (ii), we have
DC = AC + AD
= `75sqrt(3) + 25sqrt(3)`
= `100sqrt(3)`
= 100 × 1.732
= 173.2 m
Which is the required distance between two men.
RELATED QUESTIONS
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Determine the speed at which the bird flies `(sqrt(3) = 1.732)`
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
