Advertisements
Advertisements
Question
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
Solution
Consider RZ as the building, XR as the flag, and Y as the ground point from which the elevation angles are to be measured.
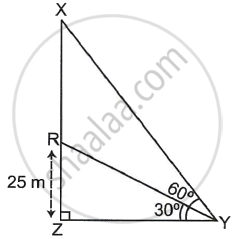
So, RZ = 25 m, ∠XYZ = 60°, ∠RYZ = 30°.
Now, in ΔRYZ,
`(RZ)/(YZ)` = tan 30°
⇒ `25/(YZ) = 1/sqrt(3)`
⇒ YZ = `25sqrt(3)` m
Also, in ΔXYZ,
`(XZ)/(YZ)` = tan 60°
`(XR + RZ)/(YZ) = sqrt(3)`
`(XR + 25)/(25sqrt(3)) = sqrt(3)`
XR + 25 = `25sqrt(3) xx sqrt(3)`
XR + 25 = 75
XR = 75 – 25 = 50
As a result, the flag's height is 50 metres.
APPEARS IN
RELATED QUESTIONS
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
From the top of a rock `50sqrt(3)` m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
In given figure, the length of AP is ____________.

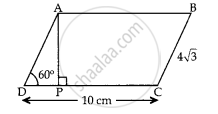
In given figure, ABCD is a || gm. The length of AP is ____________.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
