Advertisements
Advertisements
Question
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Solution
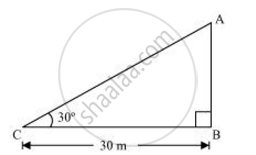
Let AB be the tower and the angle of elevation from point C (on ground) is 30°.
In ΔABC,
`("AB")/("BC") = tan 30°`
`("AB")/(30) = 1/sqrt3`
AB = `(30)/sqrt3`
AB = `(30)/sqrt3 xxsqrt3/sqrt3`
AB = `10sqrt3` m
Therefore, the height of the tower is `10sqrt3` m.
APPEARS IN
RELATED QUESTIONS
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
The ratio of the height of a tower and the length of its shadow on the ground is `sqrt3 : 1`. What is the angle of elevation of the sun?
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
The line drawn from the eye of an observer to the point in the object viewed by the observer is known as ____________.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
