Advertisements
Advertisements
Question
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
Solution
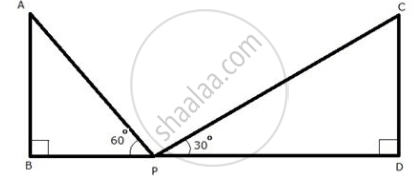
Let AB and CD be the two towers of length 'l' m.
Let P be a point in the roadway BD such that BD = 100 m, ∠APB = 60° and ∠CPD = 30°
In ΔABP,
`"AB"/"BP" = tan 60^circ`
`=> "BP" = "l"/(tan 60^circ)`
`=> "BP" = "l"/sqrt3`
In ΔCDP,
`"CD"/"DP" = tan 30^circ`
`=> "CD"/"DP" = 1/sqrt3`
`=> "l"/"DP" = 1/sqrt3`
`=> "DP" = "l" sqrt3`
`=> "DP" = "l" sqrt3`
The total width of the road is the sum of BP and PD:
∴ BP + PD = 100
∴ `l/sqrt3 + l sqrt3 = 100`
∴ `l (1/sqrt3 + sqrt3) = 100`
∴ `l (1/1.732 + 1.732) = 100` ...[Given `sqrt3` = 1.732]
∴ `l ((1 + 1.732 xx 1.732)/1.732) = 100`
∴ `l( (1 + 2.9998)/1.732) = 100`
∴ `l( (3.9998)/1.732) = 100`
∴ `100/2.309 = l`
∴ l = 43.31 m approx.
Hence, length of the piller is 43.31 m
The point is BP = `l/sqrt3`
The length of the pillars (l) and the position of point P (BP).
∴ BP = `l/sqrt3`
∴ BP = `43.31/1.732`
∴ BP = 25.00 meters.
The length of the pillars (l) and the position of point P (PD).
∴ `"DP" = "l" sqrt3`
∴ DP = 43.31 × 1.732
∴ DP = 75.01 meters.
The distance from the first pillar (associated with the 60° angle of elevation) to point P is approximately 25.00 meters.
The distance from the second pillar (associated with the 30° angle of elevation) to point P is approximately 75.01 meters.
APPEARS IN
RELATED QUESTIONS
A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
In given figure, the value of ZC is ____________.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 2m and is inclined at an angle of 30° to the ground. What should be the length of the slide?
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
