Advertisements
Advertisements
Question
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
Options
\[\left( \sqrt{3} + 1 \right) x\]
\[\left( \sqrt{3} - 1 \right) x\]
\[2\sqrt{3}x\]
\[3\sqrt{2}x\]
Solution
Let h be the height of tower AB
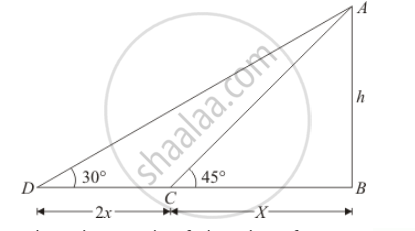
Given that: angle of elevation of sun are`∠D=30°` and.`∠C=45°`
Then Distance`CD=2x` and we assume `BC=x`Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle,`ABC`
`⇒ tan C=(AB)/(BC)`
`⇒ tan 45°=(AB)/(BC)`
`⇒ 1=h/x`
`⇒ x=h`
Again in a triangle ABD,
`⇒ tan D= (AB)/(BC+CD)`
`⇒ tan 30°=h/( x+2x)`
`⇒1/sqrt3=h/(h+2x)` `[x=h]`
`⇒ sqrt3h=h+2x`
`h(sqrt3-1)=2x`
`⇒ h=2x/(sqrt3-1)`
⇒` h=(2x)/(sqrt3-1)xx(sqrt3+1)/(sqrt3+1)`
`⇒ h=x(sqrt3+1)`
APPEARS IN
RELATED QUESTIONS
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, where as for the elder children, she wants to have a steep side at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
Two boats approach a lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the lighthouse.
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
