Question

Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is

Options

• \[\sqrt{2}a \text{ metres }\]

• \[\frac{a}{2\sqrt{2}}\text{ metres }\]

• \[\frac{a}{\sqrt{2}} \text{ metres }\]

•  2a metres

Answer 1

Let AB and CD be the two posts such that AB < CD.

Then, let AB = h so that CD = 2h

Now, the given information can be represented as,

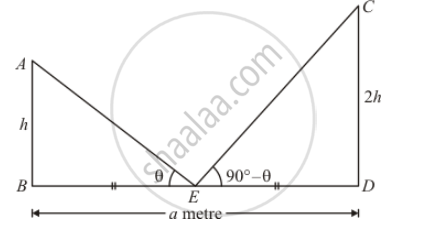
Here, E is the midpoint of BD.

We have to find height of the shorter post.

So we use trigonometric ratios.

In triangle ECD,

`⇒ tan ∠CED=(CD)/(ED)`

`⇒ tan (90°-θ)=(2h)/(a/2)` 

`⇒ cot θ=(4h)/a` 

Again in triangle ABE, 

`⇒ tan ∠AEB=AB/BE`

`⇒ tan θ=h/((a/2))`

` ⇒ 1/cotθ=(2h)/a`

`⇒ a/(4h)=(2h)/a`

`⇒ a^2=8h^2`

`⇒ h=a/(2sqrt2)`