Advertisements
Advertisements
प्रश्न
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
पर्याय
\[\sqrt{2}a \text{ metres }\]
\[\frac{a}{2\sqrt{2}}\text{ metres }\]
\[\frac{a}{\sqrt{2}} \text{ metres }\]
2a metres
उत्तर
Let AB and CD be the two posts such that AB < CD.
Then, let AB = h so that CD = 2h
Now, the given information can be represented as,
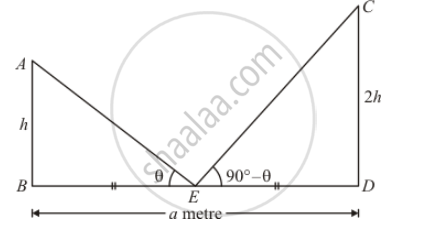
Here, E is the midpoint of BD.
We have to find height of the shorter post.
So we use trigonometric ratios.
In triangle ECD,
`⇒ tan ∠CED=(CD)/(ED)`
`⇒ tan (90°-θ)=(2h)/(a/2)`
`⇒ cot θ=(4h)/a`
Again in triangle ABE,
`⇒ tan ∠AEB=AB/BE`
`⇒ tan θ=h/((a/2))`
` ⇒ 1/cotθ=(2h)/a`
`⇒ a/(4h)=(2h)/a`
`⇒ a^2=8h^2`
`⇒ h=a/(2sqrt2)`
APPEARS IN
संबंधित प्रश्न
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
