Advertisements
Advertisements
प्रश्न
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
उत्तर
Let AD be the multistoried building of height hm. And the angle of depression of the top and bottom are 30° and 45°. We assume that BE = 8, CD = 8 and BC = x, ED = x and AC = h − 8. Here we have to find height and distance of the building.
We use trigonometric ratio.
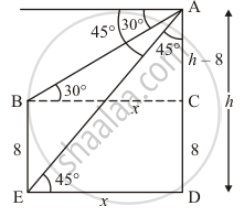
In ΔAED,
`=> tan E = (AD)/(DE)`
`=> tan 45^@= (AD)/(DE)`
`=> 1 = h/x`
=> x = h
Again in Δ ABC
`=> tan B = (AC)/(BC)`
`=> tan 30^@ = (h - 8)/x`
`=> 1/sqrt3 = (h - 8)/x`
`=> hsqrt3 - 8sqrt3 = x`
`> hsqrt3 - 8sqrt3 = h`
`=> h(sqrt3 - 1) = 8sqrt3`
`=> h = (8sqrt3)/(sqrt3 - 1) xx (sqrt3 + 1)/(sqrt3 + 1)`
`=> h = (24 + 8sqrt3)/2`
`=> h = (4(3 + sqrt3))`
And
`=> x = 4(3 + sqrt3)`
Hence the required height is `4(3 + sqrt3)` meter and distance is `4(3 + sqrt3)` meter
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
