Advertisements
Advertisements
प्रश्न
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
उत्तर
Let h be the height of light house AC. And an angle of depression of the top of light house from two ships are ∝ and ß respectively. Let` BC=x, CD=y`,. And ∠ABC =∝, ∠ADC=ß , .
We have to find distance between the ships
We have the corresponding figure as follows
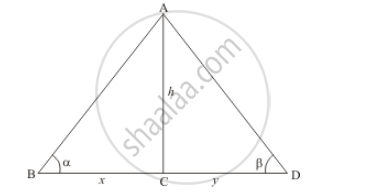
We use trigonometric ratios.
In `Δ ABC`
⇒` tan ∝ =(AC)/(BC)`
⇒` tan ∝= h/x`
⇒` x= h/ tan ∝`
Again in `Δ ADC`
⇒ `tan ß=(AC)/(CD)`
⇒` tan ß= h/y`
⇒` y=h/tan ß`
Now,
⇒ `BD=x+y`
⇒ `BD= h/tan ∝ +h/tan ß`
⇒ `BD= (h(tan∝+tan ß ))/(tan ∝ tanß)`
Hence the distance between ships is `(h(tan∝+tan ß))/(tan∝ tan ß)`
APPEARS IN
संबंधित प्रश्न
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 2m and is inclined at an angle of 30° to the ground. What should be the length of the slide?
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
