Advertisements
Advertisements
प्रश्न
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
उत्तर
Given: the height of tower is h m.
∠ABD = α and ∠ACD = β
Let CD = y and BC = x

In ∆ABD,
tan α = `"AD"/"BD"`
⇒ tan α = `"h"/("BC" + "CD")`
⇒ tan α = `"h"/(x + y)`
⇒ x + y = `"h"/tan α`
⇒ y = `"h"/tan α - x` ...[Equation 1]
In ∆ACD,
tan β = `"AD"/"CD"`
⇒ tan β = `"h"/y`
⇒ y = `"h"/tan β` ...[Equation 2]
Comparing equation 1 and equation 2,
`"h"/tan α - x = "h"/tan β`
⇒ x = `"h"/tan α - "h"/tan β`
⇒ x = `"h"(1/tan α - 1/tan β)`
⇒ x = h(cot α – cot β)
Hence, we have got the required distance between the two points, i.e. h(cot α – cot β)
APPEARS IN
संबंधित प्रश्न
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

Read the following passage and answer the questions given below.
|
Kite Festival Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites. The picture given below, show three kites flying together.
In the given figure, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find. |
- the lengths of strings used (take them straight) for kites A and B as shown in the figure.
- the distance 'd' between these two kites.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
|
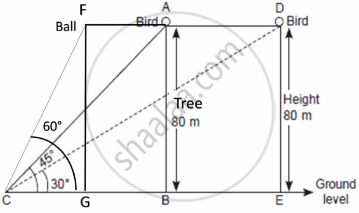
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?