Advertisements
Advertisements
प्रश्न
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
उत्तर
Let OP be the tree and A, B be the two points such OA = a and OB = b and angle of elevation to the tops are α and β respectively.
Let OL = x and PL = h
We have to prove the following
`h = ((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
The corresponding figure is as follows
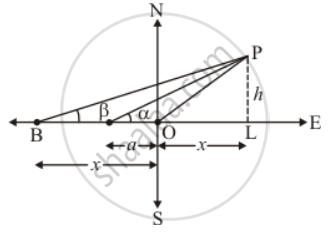
In ΔALP
`=> tan alpha = (PL)/(OA + OL)`
`=> tan alpha = h/(a + x)`
`=> 1/(cot alpha) = h/(a + x)`
`=> h cot alpha = a + x`.....(1)
Again in ΔBLP
`=> tan beta = (PL)/(OB + OL)`
`=> tan beta = h/(b + x)`
`=> 1/(cot beta) = h/(b + x)`
`=> h cot beta = b + x` .....(2)
Subtracting equation (1) from (2) we get
`=> h cot beta - hcot alpha = b - a`
`=> h(cot beta - cot alpha) = b - a`
`=> h (b -a)/(cot beta - cot alpha)`
`h = ((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
Hence height of the top from ground is `h = ((b -a) tan alpha tan beta)/((tan alpha - tan beta))`
APPEARS IN
संबंधित प्रश्न
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
A vessel full of water is in the form of an inverted cone of height 8 cm and the radius of its top, which is open, is 5 cm. 100 spherical lead balls are dropped into the vessel. One-fourth of the water flows out of the vessel. Find the radius of a spherical ball ?
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
