Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
उत्तर
Let PQ be the tower of height H m and an angle of elevation of the top of tower PQ from point X is 60°. An angle of elevation at 40 m vertical from point X is 45°.
Let PQ = H m and SX = 40m. OX = x, ∠PST = 45°, ∠PXQ = 60°
Here we have to find height of tower.
The corresponding figure is as follows
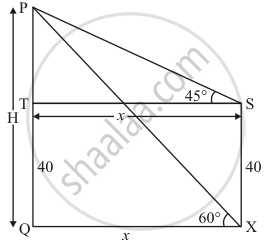
We use trigonometric ratios.
In ΔPST
`=> tan 45^@ = h/x`
`=> 1 = h/x`
`=> x = h`
Again in ΔPST
`=> tan 456@ = h/x`
`=> 1 = h/x`
`=> x = h`
Again in ΔPXQ
`=> tan 60^@ = (h + 40)/x`
`=> sqrt3 = (h + 40)/x`
`=> h + 40 = sqrt3h`
`=> h(sqrt3 - ) = 40`
`=> h = 40/(sqrt3 - 1)`
`=> h = 54.64`
Therefore `H = 54.64 + 40`
`=> H = 94.64`
Hence the height of tower uis 94.64 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
In given figure, the value of CE is ____________.
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
