Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
उत्तर
Let PQ be the tower of height H m and an angle of elevation of the top of tower PQ from point X is 60°. An angle of elevation at 40 m vertical from point X is 45°.
Let PQ = H m and SX = 40m. OX = x, ∠PST = 45°, ∠PXQ = 60°
Here we have to find height of tower.
The corresponding figure is as follows
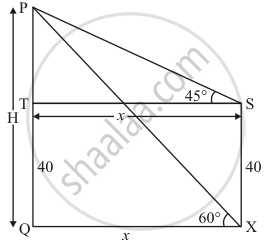
We use trigonometric ratios.
In ΔPST
`=> tan 45^@ = h/x`
`=> 1 = h/x`
`=> x = h`
Again in ΔPST
`=> tan 456@ = h/x`
`=> 1 = h/x`
`=> x = h`
Again in ΔPXQ
`=> tan 60^@ = (h + 40)/x`
`=> sqrt3 = (h + 40)/x`
`=> h + 40 = sqrt3h`
`=> h(sqrt3 - ) = 40`
`=> h = 40/(sqrt3 - 1)`
`=> h = 54.64`
Therefore `H = 54.64 + 40`
`=> H = 94.64`
Hence the height of tower uis 94.64 m
APPEARS IN
संबंधित प्रश्न
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. `(sqrt(3) = 1.732)`
In given figure, the value of CE is ____________.
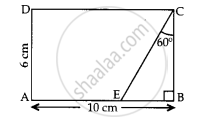
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
