Advertisements
Advertisements
प्रश्न
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
उत्तर
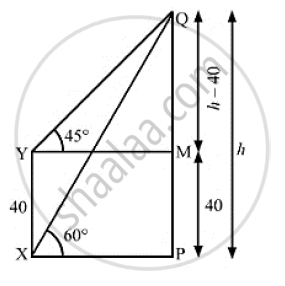
We have
XY = 40m,∠PXQ = 60° and ∠MYQ = 45°
Let PQ = h
Also, MP = XY = 40m, MQ = PQ - MP = h - 40
In ΔMYQ,
` tan 45° = (MQ)/(MY)`
`⇒1 = (h-40)/(MY)`
⇒ MY = H - 40
⇒ PX = MY = h - 40 ................(1)
Now , in ΔMXQ,
`tan 60° = (PQ)/(PX)`
`⇒ sqrt(3) = h/( h-40)` [From (i)]
`⇒ h sqrt(3) - 40 sqrt(3) = h `
`⇒ h sqrt(3) -h = 40 sqrt(3)`
`⇒ h (sqrt(3)-1) = 40 sqrt(3)`
`⇒ h = (40sqrt(3))/((sqrt(3)-1))`
`⇒ h = (40 sqrt(3))/((sqrt (3)-1)) xx ((sqrt(3)+1))/((sqrt(3)+1))`
`⇒ h = (40 sqrt(3)(sqrt(3)+1))/((3-1))`
`⇒h = (40 sqrt(3) ( sqrt(3) +1))/2`
`⇒h= 20sqrt(3) (sqrt(3)+1)`
`⇒ h= 60+20 sqrt(3)`
`⇒ h= 60+20xx 1.73`
`⇒h = 60+ 34.6`
∴ h = 94.6m
So, the height of the tower PQ is 94. 6 m.
APPEARS IN
संबंधित प्रश्न
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ


