Advertisements
Advertisements
प्रश्न
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
उत्तर
Let AB be the balloon of height h. And the balloon is connected to the metrological ground station by a cable of length 215 m. Let AC = 215 and `∠ACB = 60^@`
Here we have to find the height of balloon.
We have the following corresponding figure
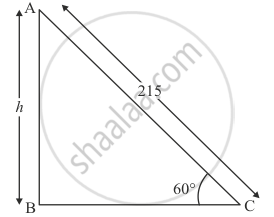
So we use trigonometric ratios
In a triangle ABC
`=> sin C = (AB)/(AC)`
`=> sin 60^@ = h/215`
`=> sqrt3/2 = h/215`
`=> h = 186`
Hence the height of balloon is 186 m
APPEARS IN
संबंधित प्रश्न
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Find the speed of flying of the bird.
`("Take"sqrt3=1.732)`
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
