Advertisements
Advertisements
प्रश्न
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Find the speed of flying of the bird.
`("Take"sqrt3=1.732)`
उत्तर
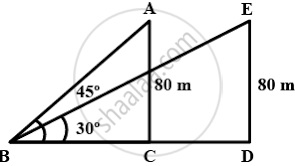
`tan 45° = (AC)/(BC)`
`1 = 80/(BC)`
BC = 80 cm
`tan 30° = (DE)/(BC+CE)`
`1/sqrt3 = 80/(80+x)`
80 + x = 80 √3
x = 80 √3 − 80
x = 80 (√3 − 1) m
The bird travelled 80 (√3 − 1) m
Speed of bird = `"Distance"/"Time"`
`= 40 (sqrt3-1)/2`
= 40 (√3 − 1) m/s
∴ Speed = 40 (√3 − 1) m/s,
संबंधित प्रश्न
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
The angles of elevation of the top of a tower from two points distant s and t from its foot are complementary. Then the height of the tower is ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is ______.
