Advertisements
Advertisements
प्रश्न
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
विकल्प
60°
45°
30°
90°
उत्तर
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is 60°.
Explanation:
Let BC = 6 m be the height of the pole and AB = `2sqrt(3)` m be the length of the shadow on the ground.
Let the Sun's makes an angle θ on the ground.
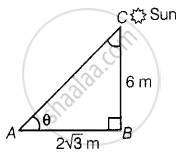
Now, In ΔABC,
tan θ = `"BC"/"AB"`
⇒ tan θ = `6/(2sqrt(3))`
= `3/sqrt(3) * sqrt(3)/sqrt(3)`
⇒ tan θ = `(3sqrt(3))/3`
= `sqrt(3)` ...`[∵ tan 60^circ = sqrt(3)]`
= tan 60°
∴ θ = 60°
Hence, the Sun's elevation is 60°.
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
Find the distance between the points (a, b) and (−a, −b).
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
