Advertisements
Advertisements
Question
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
Options
60°
45°
30°
90°
Solution
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is 60°.
Explanation:
Let BC = 6 m be the height of the pole and AB = `2sqrt(3)` m be the length of the shadow on the ground.
Let the Sun's makes an angle θ on the ground.
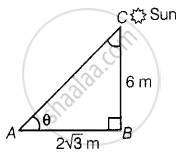
Now, In ΔABC,
tan θ = `"BC"/"AB"`
⇒ tan θ = `6/(2sqrt(3))`
= `3/sqrt(3) * sqrt(3)/sqrt(3)`
⇒ tan θ = `(3sqrt(3))/3`
= `sqrt(3)` ...`[∵ tan 60^circ = sqrt(3)]`
= tan 60°
∴ θ = 60°
Hence, the Sun's elevation is 60°.
APPEARS IN
RELATED QUESTIONS
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
Find the distance between the points (a, b) and (−a, −b).
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
