Advertisements
Advertisements
Question
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
Solution
Height of the statue = 1.6 m
Let the height of the pedestal be “h”
AD = H + 1.6 m
Let AB be x
In the right ∆ABD, tan 60° = `"AD"/"AB"`
`sqrt(3) = ("h" + 1.6)/x`
x = `("h" + 1.6)/sqrt(3)` ...(1)
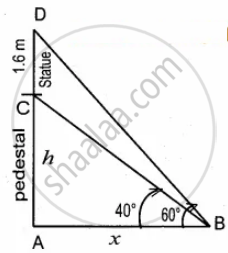
In the right ∆ABC, tan 40° = `"AC"/"AB"`
0.8391 = `"h"/x`
x = `"h"/(0.8391)`
Substitute the value of x in (1)
`"h"/(0.8391) = ("h" + 1.6)/sqrt(3)`
(h + 1.6) 0.8391 = `sqrt(3)` h
0.8391 h + 1.34 = 1.732 h
1.34 = 1.732 h – 0.8391 h
1.34 = 0.89 h
h = `1.34/0.89`
= `134/89`
= 1.5 m
Height of the pedestal = 1.5 m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
The shadow of a building is 20 m long when the angle of elevation of the sun is 60º. Find the height of the building
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
