Advertisements
Advertisements
प्रश्न
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
उत्तर
Height of the statue = 1.6 m
Let the height of the pedestal be “h”
AD = H + 1.6 m
Let AB be x
In the right ∆ABD, tan 60° = `"AD"/"AB"`
`sqrt(3) = ("h" + 1.6)/x`
x = `("h" + 1.6)/sqrt(3)` ...(1)
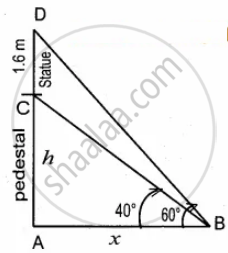
In the right ∆ABC, tan 40° = `"AC"/"AB"`
0.8391 = `"h"/x`
x = `"h"/(0.8391)`
Substitute the value of x in (1)
`"h"/(0.8391) = ("h" + 1.6)/sqrt(3)`
(h + 1.6) 0.8391 = `sqrt(3)` h
0.8391 h + 1.34 = 1.732 h
1.34 = 1.732 h – 0.8391 h
1.34 = 0.89 h
h = `1.34/0.89`
= `134/89`
= 1.5 m
Height of the pedestal = 1.5 m
APPEARS IN
संबंधित प्रश्न
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
If a tower 30 m high, casts a shadow `10sqrt3` m long on the ground, then what is the angle of elevation of the sun?
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
In given figure, the value of AE is ____________.
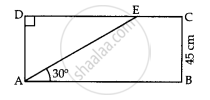
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
