Question

Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.

पर्याय

• `"h"/2` m

• `"h"/3` m

• `sqrt3  "h"`m

• `"h"/sqrt3  "m"`

Answer 1

Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is `underline("h"/3)` m.

Explanation:

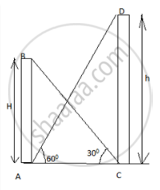
Let the height of tower A be = AB = H.

And the height of tower B = CD = h

In triangle ABC

tan30° = AB/AC = H/AC …….(1)

In triangle ADC

tan60° = CD/AC = h/AC …….(2)

Divide (1) by (2)

We get tan30°/tan60° = H/h

H = h/3