Advertisements
Advertisements
प्रश्न
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
उत्तर
Let SQ = h be the tower.
∠SPQ = 30° and ∠SRQ = 60°
According to the question,
The length of shadow is 50 m long the angle of elevation of the sun is 30° than when it was 60°.
So, PR = 50 m and RQ = x m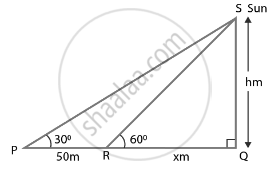
So in ∆SRQ, we have
tan 60° = `"h"/x` ...`[∵ tan θ = "perpendicular"/"base" ⇒ tan 60^circ = "SQ"/"RQ"]`
⇒ `sqrt(3) = "h"/x` ...`[∵ tan 60^circ = sqrt(3)]`
⇒ `x = "h"/sqrt(3)`
In ΔSPQ,
tan 30° = `"h"/(50 + x)` ...`[∵ tan 30^circ = "SQ"/"PQ" = "SQ"/("PR" + "PQ")]`
⇒ `1/sqrt(3) = "h"/(50 + x)` ...`[∵ tan 30^circ = 1/sqrt(3)]`
⇒ `50 + x = sqrt(3)"h"`
Substituting the value of x in the above equation, we get
⇒ `50 + "h"/sqrt(3) = sqrt(3)"h"`
⇒ `(50sqrt(3) + "h")/sqrt(3) = sqrt(3)"h"`
⇒ `50sqrt(3) + "h" = 3"h"`
⇒ `50sqrt(3) = 3"h" - "h"`
⇒ `3"h" - "h" = 50sqrt(3)`
⇒ 2h = `50sqrt(3)`
⇒ h = `(50sqrt(3))/2`
⇒ h = `25sqrt(3)`
Hence, the required height is `25sqrt(3) "m"`.
APPEARS IN
संबंधित प्रश्न
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°, then the distance between the two towers is ____________.
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]

