Advertisements
Advertisements
Question
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
Solution
Let SQ = h be the tower.
∠SPQ = 30° and ∠SRQ = 60°
According to the question,
The length of shadow is 50 m long the angle of elevation of the sun is 30° than when it was 60°.
So, PR = 50 m and RQ = x m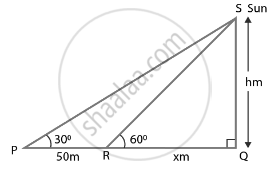
So in ∆SRQ, we have
tan 60° = `"h"/x` ...`[∵ tan θ = "perpendicular"/"base" ⇒ tan 60^circ = "SQ"/"RQ"]`
⇒ `sqrt(3) = "h"/x` ...`[∵ tan 60^circ = sqrt(3)]`
⇒ `x = "h"/sqrt(3)`
In ΔSPQ,
tan 30° = `"h"/(50 + x)` ...`[∵ tan 30^circ = "SQ"/"PQ" = "SQ"/("PR" + "PQ")]`
⇒ `1/sqrt(3) = "h"/(50 + x)` ...`[∵ tan 30^circ = 1/sqrt(3)]`
⇒ `50 + x = sqrt(3)"h"`
Substituting the value of x in the above equation, we get
⇒ `50 + "h"/sqrt(3) = sqrt(3)"h"`
⇒ `(50sqrt(3) + "h")/sqrt(3) = sqrt(3)"h"`
⇒ `50sqrt(3) + "h" = 3"h"`
⇒ `50sqrt(3) = 3"h" - "h"`
⇒ `3"h" - "h" = 50sqrt(3)`
⇒ 2h = `50sqrt(3)`
⇒ h = `(50sqrt(3))/2`
⇒ h = `25sqrt(3)`
Hence, the required height is `25sqrt(3) "m"`.
APPEARS IN
RELATED QUESTIONS
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
