Advertisements
Advertisements
Question
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
Solution
Let the height of the tower is h.
And ∠ABC = θ
Given that, BC = s, PC = t
And angle of elevation on both positions are complementary.
i.e., ∠APC = 90° – θ ...[If two angles are complementary to each other, then the sum of both angles is equal to 90°]
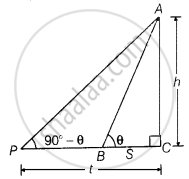
Now in ΔABC,
tan θ = `"AC"/"BC" = "h"/"s"` ...(i)
And in ΔAPC,
tan(90° – θ) = `"AC"/"PC"` ...[∵ tan(90° – θ) = cot θ]
⇒ cot θ = `"h"/"t"`
⇒ `1/tanθ = "h"/"t"` `[∵ cot θ = 1/tan θ]` ...(ii)
On, multiplying equations (i) and (ii), we get
`tan θ * 1/tanθ = "h"/"s" * "h"/"t"`
⇒ `"h"^2/("st")` = 1
⇒ h2 = st
⇒ h = `sqrt("st")`
So, the required height of the tower is `sqrt("st")`.
Hence proved.
APPEARS IN
RELATED QUESTIONS
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
An observer , 1.7 m tall , is` 20 sqrt3` m away from a tower . The angle of elevation from the eye of an observer to the top of tower is 300 . Find the height of the tower.
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
The angle of elevation of the top of a 30 m high tower at a point 30 m away from the base of the tower is ______.
