Advertisements
Advertisements
Question
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
Solution
Let AB be the lighthouse of 150 m. and angle of depression of two ship C and D are 30° and 45° respectively.
let BC = x,CD = y and ∠ADB = 30°, ∠ACB = 45°
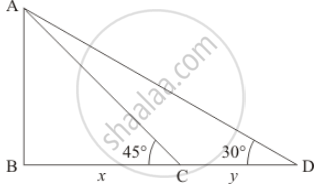
We use trigonometric ratios.
IN a triangle ABC
`=> tan 45^@ = (AB)/(BC)`
`=> 1 = 150/x`
`=> x = 150`
Again in a triangle ABD
`=> tan 30° = (AB)/(BD)`
`=> 1/sqrt3 = 150/(x + y)`
`=> x + y = 150sqrt3`
`=> 150 + y = 150sqrt3`
`=> y = 150sqrt3 - 150`
`=> y = 150(sqrt3 - 1)`
`=> y = 150 xx 0.732`
Hence distance between the ships is 109.8 m
APPEARS IN
RELATED QUESTIONS
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
In given figure, the length of AP is ____________.

An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is ______.
