Advertisements
Advertisements
Question
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
Options
True
False
Solution
This statement is True.
Explanation:
Case (i): Let the height of a tower be h and the distance of the point of observation from its foot is x.
In ∆ABC,
tan θ1 = `"AC"/"BC" = "h"/x` ...(i)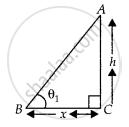
Case (ii): Now, the height of a tower increased by 10%
= h + 10% of h
= `"h" + "h" * 10/100`
= `(11"h")/100`
And the distance of the point of observation from its foot
= x + 10% of x
= `x + x xx 10/100 = (11x)/10`
In ΔPQR,
tan θ2 = `"PR"/"QR" = (((11"h")/10))/(((11x)/10))`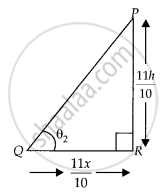
⇒ tan θ2 = `"h"/x` ...(ii)
From equations (i) and (ii), we get
tan θ1 = tan θ2
⇒ θ1 = θ2
Hence, the required angle of elevation of its top remains unchanged.
APPEARS IN
RELATED QUESTIONS
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
In given figure, the value of CE is ____________.
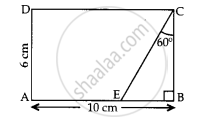
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
