Advertisements
Advertisements
Question
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
Solution
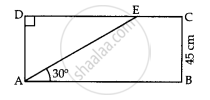
Let AB be the height of the observer and EC be the height of the tower.
Given:
AB = 1.7 m ⇒ CD = 1.7 m
BC = 203-\[\sqrt{3}\] m
Let ED be h m.

In ∆ADE,
\[\tan 30^o = \frac{ED}{AD}\]
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{h}{20\sqrt{3}}\]
\[ \Rightarrow h = 20 m\]
Hence, the height of the tower is 21.7 m.
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
In given figure, the value of AE is ____________.