Advertisements
Advertisements
Question
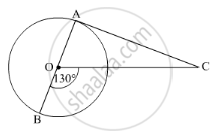
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.
Solution
In the given figure,
\[ \Rightarrow \angle AOC = 180^o - 130^o = 50^o\]
\[ \Rightarrow \angle AOC = 180^0- 130^o = 50^0\] (Because the tangent at any point of a circle is perpendicular to the radius through the point of contact)
\[\angle AOC + \angle CAO + \angle ACO = 180^o \left( \text{Angle sum property of a triangle} \right)\]
\[\angle AOC + \angle CAO + \angle ACO = 180^o\left( \text{Angle sum property of a triangle} \right)\]
APPEARS IN
RELATED QUESTIONS
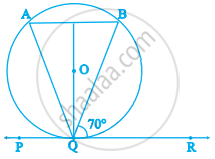
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

A circle can have ______ parallel tangents at the most.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
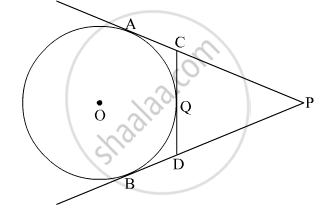
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
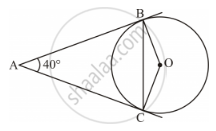
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
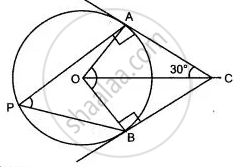
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.