Advertisements
Advertisements
प्रश्न
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

उत्तर
In the given figure,
\[ \Rightarrow \angle AOC = 180^o - 130^o = 50^o\]
\[ \Rightarrow \angle AOC = 180^0- 130^o = 50^0\] (Because the tangent at any point of a circle is perpendicular to the radius through the point of contact)
\[\angle AOC + \angle CAO + \angle ACO = 180^o \left( \text{Angle sum property of a triangle} \right)\]
\[\angle AOC + \angle CAO + \angle ACO = 180^o\left( \text{Angle sum property of a triangle} \right)\]
APPEARS IN
संबंधित प्रश्न
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
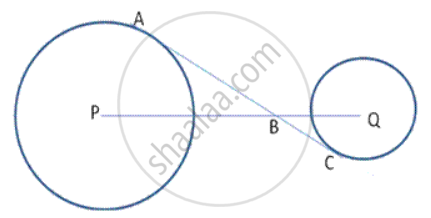
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

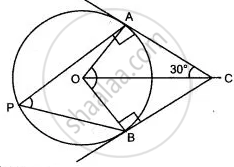
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
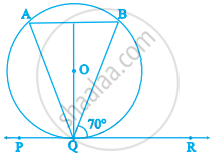
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

