Advertisements
Advertisements
प्रश्न
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

उत्तर
Since lengths of the tangents drawn from an exterior point to a circle are equal.
∴ AF = AE ...(i)
BD = BF ...(ii)
and CE = CD ...(iii)
Adding (i), (ii) and (iii), we get
AF + BD + CE = AE + BF + CD
Now, Perimeter of Δ ABC = AB + BC + AC
= (AF + FB) + (BD + CD) + (AE + EC)
= (AF + AE) + (BD + BF) + (CD + CE)
= 2AF + 2BD + 2CE
= 2( AF + BD + CE) ....(From (i), (ii) and (iii), we get AE = AF, BD = BF, and CD = CE)
∴ AF + BD + CE = `1/2`( Perimeter of ΔABC)
∴ AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)
Hence proved.
APPEARS IN
संबंधित प्रश्न
A tangent to a circle intersects it in ______ point (s).
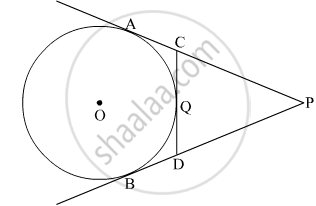
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

