Advertisements
Advertisements
प्रश्न
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

उत्तर
In order to prove that ΔADT is isosceles i.e., TA = TD, it is sufficient to show that ∠TAD = ∠TDA.
Since ∠TAB and ∠BCA are angles in the alternate segments of chord AB.
∴ ∠TAB = ∠BCA ...(i)
It is given that AD is the bisector of ∠BAC.
∠BAD = ∠CAD ...(ii)
Now, ∠TAD = ∠TAB + ∠BAD
⇒ ∠TAD = ∠BCA + ∠CAD ....(Using (i) and (ii))
⇒ ∠TAD = ∠DCA + ∠CAD ....( ∵∠BCA = ∠DCA)
⇒ ∠TAD = 180° - ∠CAD ....( In ΔCAD, ∠CAD + ∠DCA +∠CDA = 180° ∴ ∠CAD + ∠BCA = 180° - ∠CAD)
⇒ ∠TAD = ∠TDA ....(∵∠CDA + ∠TDA = 180°)
= TD = TA
Hence, ΔADT is isosceles
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
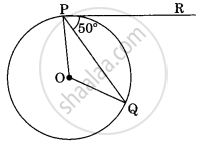
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
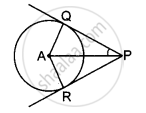
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
