Advertisements
Advertisements
प्रश्न
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
उत्तर
Rough Figure:
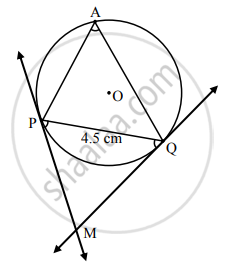
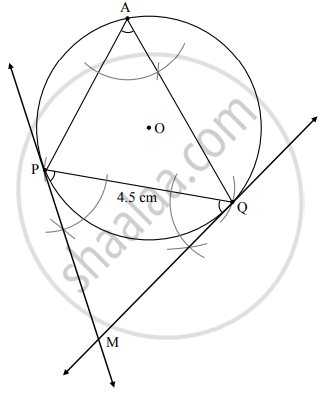
Steps of construction:
- Draw a circle of radius 2.7 cm.
- Draw a chord PQ of length 4.5 cm.
- Take a point A on the major arc, other than P and Q.
- Join PA and QA.
- Using P and Q as vertices and chord PQ as one side, draw ∠MPQ and ∠MQP equal to ∠PAQ.
- Lines containing the rays PM and QM are the tangents to the circle at P and Q respectively.
APPEARS IN
संबंधित प्रश्न
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = Scm, find PT.
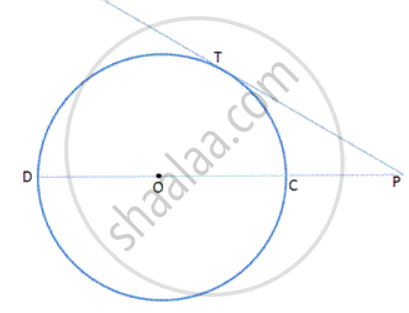
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
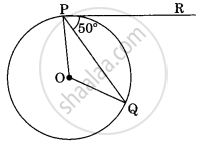
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
Tangents from an external point to a circle are ______
Find the value of ∠DCE.

ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
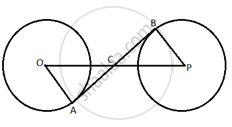
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
