Advertisements
Advertisements
प्रश्न
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
विकल्प
4 cm
5 cm
6 cm
8 cm
उत्तर
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is 8 cm.
Explanation:
First, draw a circle of radius 5 cm with centre O.
A tangent XY is drawn at point A.
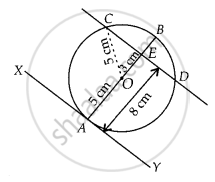
A chord CD is drawn which is parallel to XY and at a distance of 8 cm from A.
Now, ∠OAY = 90° ...[∵ Tangent at any point of circle is perpendicular to the radius through the point of contact]
∠OAY + ∠OED = 180° ...[∵ Sum of cointerior angles is 180°]
⇒ ∠OED = 180° – 90° = 90°
Also, AE = 8 cm.
Join OC
OC = 5 cm ...[Radius of circle]
OE = AE – OA
= 8 – 5
= 3 cm
Now, in right angled ∆OEC,
OC2 = OE2 + EC2 ...[By Pythagoras theorem]
⇒ EC2 = OC2 – OE2
⇒ EC2 = 52 – 32
⇒ EC2 = 25 – 9 = 16
⇒ EC = 4 cm
Since, perpendicular from centre to the chord bisects the chord.
∴ CE = ED
⇒ CD = 2 × EC
⇒ CD = 2 × 4
⇒ CD = 8 cm
APPEARS IN
संबंधित प्रश्न
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

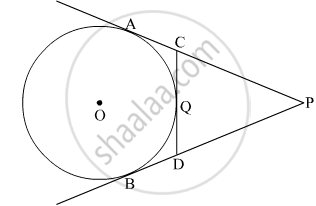
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
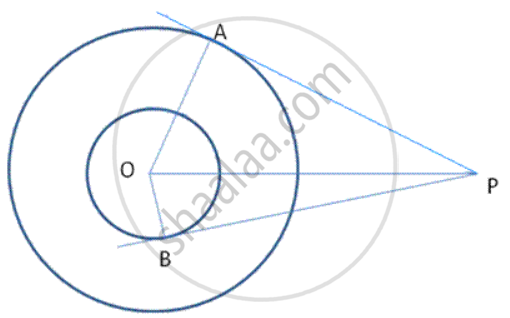
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

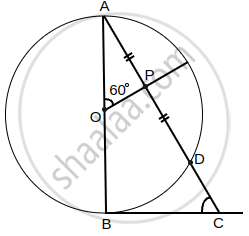
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.